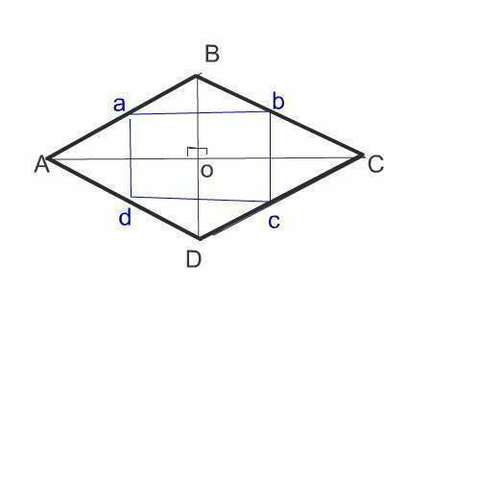
Все стороны ромба равны между собой.
Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам.
Рассмотрим рисунок к задаче.
Стороны четырехугольника abcd - средние линии треугольников, образованных сторонами ромба и их диагоналями.
Пусть аd=х
Пусть dc=у
Поскольку аd=ВО ( половине ВD), а
dc=АО (половине АС)
то ВО=х
АО=у
Тогда из прямоугольного треугольника АВО
х² +у² =30²
Полупериметр прямоугольника abcd=84:2=42
х+у=84:2=42
Выразим у через х
у=42-х
Подставим это значение в первое уравнение:
х² +(42-х)² =30²
х²+1764-84х+х²=900
2х²-84х+864=0
По формуле неприведенного квадратного уравнения ( можно и через дискриминант) найдем х
..................________
x = (-b ± √(b² - 4ac)) / 2a
x = (84 ± √‾(7056 - 6912)) / 4
х1=24
х2=18
Пусть х=24 тогда
у=42-24=18
S abcd=18*24=432