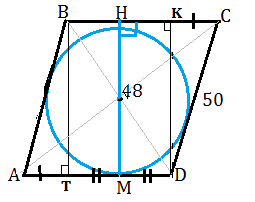
На рисунке, данном в приложении, ромб АВСD.
Диаметр НМ вписанной окружности перпендикулярен его сторонам и равен 2r=48 см
Из В и D проведем перпендикуляры ВТ и КD к противоположным сторонам ромба. Они равны диаметру вписанной окружности и являются высотами ромба.
Треугольники АВТ и КСD равны по гипотенузе и острому углу. Следовательно, АТ=КС
АТ=√(АВ²-ВТ²)=14 см
ТD=50-14=36 см
НМ проходит через центр вписанной окружности (диаметр) и делит ТD пополам.
МД=36:2=18 см
АМ=50-18=32 см
!8 см и 32 см - отрезки, на какие делит сторону данного ромба точка касания вписанного в него круга.