Помогииитеее пожалуйста))))))))))Дан прямоугольный треугольник АВС, угол В равен 90...

Question 1

Помогииитеее пожалуйста))))))))))Дан прямоугольный треугольник АВС, угол В равен 90 градусов, высота ВД=24 см , сторона ДС равна 18 см. найти АВ, сos А?

Question 2

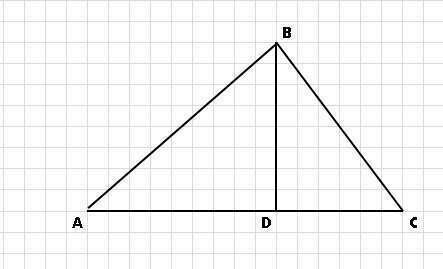
Квадрат высоты прямоугольного треугольника, проведенной из вершины прямого угла, равен произведению проекций катетов, то есть

BD^2 = AD * CD

Отсюда AD = BD^2 / CD = 24^2 / 18 = 32

Гипотенуза AC = AD + CD = 32 + 18 = 50

Из треугольника CDB по теореме Пифагора находим:

$BC = \sqrt{BD^{2} + CD^{2}} = \sqrt{24^{2} + 18^{2}} = 30$

Из треугольника ABC по теореме Пифагора находим:

$AB = \sqrt{AC^{2} - BC^{2}} = \sqrt{50^{2} - 30^{2}} = 40$

$Cos A = \frac{AB}{AC} = \frac{40}{50} = 0.8$

Ответ: AB = 40; Cos A = 0,8

Alphaeus_zn · Answer 1 · 2018-03-06T05:58:32+0000