Переносим куб из степени вперед по свойству логарифма:
log^(5-x) по 2 - 6 log (5-x) по 2 + 9
Вводим функцию, у = log^(5-x) по 2 - 6 log (5-x) по 2 + 9
Приравниваем к нулю = log^(5-x) по 2 - 6 log (5-x) по 2 + 9 = 0
теперь вводим новую переменную => log (5-x) по 2 = t
переписываем с t = t^2 - 6t + 9 = 0
Решаем уравнение:
Дискриминант: 36 - 36 = 0
t = 6+0/2 => t = 3
Приравниваем: log (5-x) по 2 = 3
находим х
2^3 = 5 - х
5 - х = 8
- х = 3
х = - 3
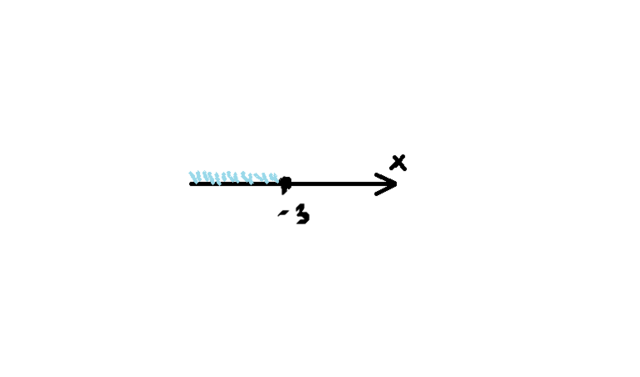
Теперь строим координатный луч и отмечаем на нем точку х = - 3 (точка закрашенная, т. к. меньше равно)
И закрашиваем промежуток, которому принадлежат значения х.
Ответ: х принадлежит (- бесконечности; -3]