Я уже отвечал на этот вопрос. Повторю:
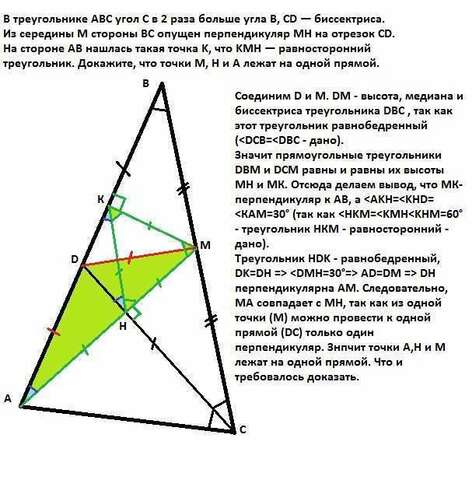
Соединим D и М. DM - высота, медиана и биссектриса треугольника DBC ,
так как этот треугольник равнобедренный (Значит
прямоугольные треугольники DBM и DCM равны и равны их высоты МН и МК.
Отсюда делаем вывод, что МК-перпендикуляр к АВ, а
Треугольник HDK -
равнобедренный, DK=DH => AD=DM => DH
перпендикулярна АМ. Следовательно, МА совпадает с МН, так как из одной
точки (М) можно провести к одной прямой (DC) только один перпендикуляр.
Значит точки А,Н и М лежат на одной прямой.
Что и требовалось доказать.