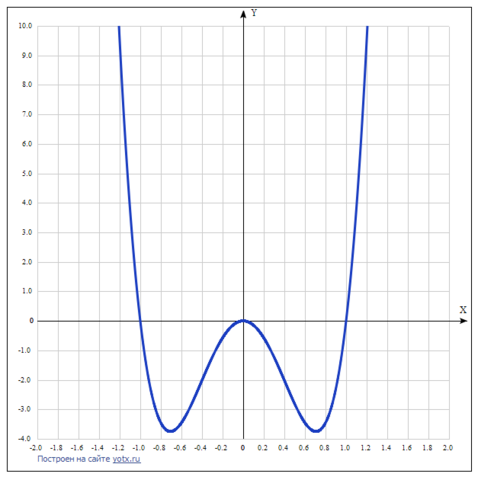
Для функции y=15x^4-15x^2 такие параметры:1) D(y) = R.
2) E(y) = R.
3) Количество нулей функции - 3.
4) Функция чётная (переменная в чётной степени).
5) Количество промежутков знакопостоянства:
у > 0 - 2
y < 0 - 2.
6) Производная равна y' = 60x³ - 30x.
Приравниваем нулю: 60x³ - 30x = 0
30х(2х² - 1) = 0
х₁ = 0
2х² - 1 = 0
х² = 1/2
х = √(1/2) = +-(1 / √2)
х₂ = 1 / √2
х₃ = -1 / √2.
у↑(-1 / √2...0), (1 / √2...∞)
у↓(-∞...-1 / √2), (0...1 / √2)
7) х = -1 / √2 и х = 1 / √2 это минимумы функции
х = 0 это локальный максимум функции.
у(-1 / √2) и у(1 / √2) = -3,75,
у(0) = 0.
8) Наибольшего значения функции нет.
Наименьшее равно -3,75.