Помогите исследовать функцию

Question

Дано ответов: 2

Правильный ответ

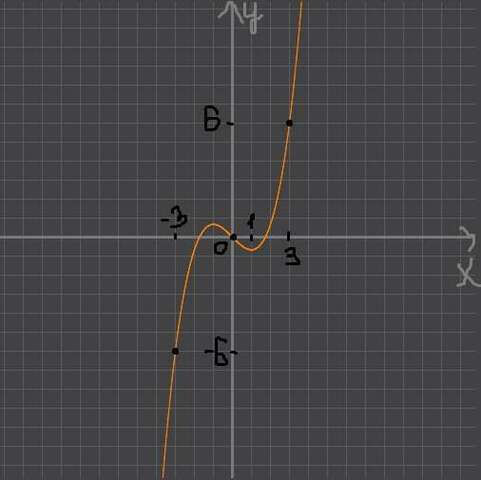
$y= \frac{1}{3} x^3-x$ (см. график функции, первая картинка)

1) Найдём производную функции:
$y'=(\frac{1}{3} x^3)'-(x)'=x^2-1$

2) Приравняем значение производной к нулю, решим уравнение, и найдем экстремумы функции:
$x^2-1=0 \\ x^2=1 \\ x=б1$

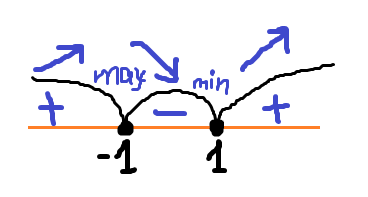
3) Нанесём на числовую прямую найденные точки   $-1$ и   $1$ . (см. рисунок, вторая картинка)
Выясним знаки производной на каждом промежутке.
Там где знак плюс, значит функция возрастает, где минус - убывает. Видно по графику, что $y$ ↑  при $x\in(-\infty;-1)\text{ U }(1;+\infty)$ и $y$ ↓ при $x\in(-1;1)$ .   (Это как раз ответ на вопрос омонотонности).
Где знак переходит из плюса в минус, эта точка будет точкой максимума. В нашем случае эта точка $(-1;0)$
Где - из минуса в плюс, значит это точка минимума. ( $(1;0)$ )

Ответ: 1) точки экстремума $(-1;0)$ и $(1;0)$ ;
  2) $y$ ↑  при $x\in(-\infty;-1)\text{ U }(1;+\infty)$ ;
     $y$ ↓ при $x\in(-1;1)$ .

wangross_zn (23.5k баллов) 13 Апр, 18

аноним · Answer 1 · 2018-04-13T00:18:24+0000

Y=1/3*x²-x
D(y)∈(-∞;∞)
y(-x)=-1/3*x³+x=-(1/3*x³-x) нечетная,значит симметричная началу координат
x=0 y=0
y=0 x(1/3*x²-1)=0 x=0 x=-√3 x=√3
(0;0);(-√3;0);(√3;0)-точки пересечения с осями
y`=x²-1=0
x=-1 x=1
+ _ +
-------------(-1)------------(1)-----------------
возр max убыв min возр
ymax=2/3
ymin=-2/3
y``=2x=0
x=0
_ +
-------------------(0)----------------------
выпук вверх вогнута вниз
(0;0)-точка перегиба