С пунктом 2 всё просто. Так как радиус - величина постоянная, то расстояние от центра окружности до продолжения сторон одинаковые, а, как мы знаем, это свойство биссектрисы угла треугольника, то есть медиана является и биссектрисой, так как это справедливо для всех сторон и углов треугольника, то три стороны равны, а треугольник - равносторонний.
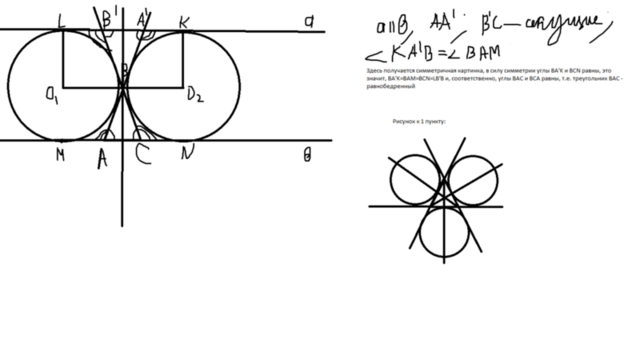
С пунктом 1 чуть потруднее. В рисунке есть обозначения, которые помогут разобраться. В чём суть: есть прямая, которой касаются две окружности равных радиусов (с одной стороны). Значит, существует прямая, параллельная данной, которой так же с одной стороны будут касаться обе заданные окружности (она, кстати, находится на расстоянии 2R от первой прямой). Используя секущие при параллельных прямых, рассматриваем равные углы и смежные с ними, в итоге приходим к тому, что 2 угла у треугольника ABC равны, и, следовательно, он равнобедренный.