Через точку пересечения биссектрис ВВ1 и СС1 треугольника ABC проведена прямая,...

Question

Через точку пересечения биссектрис ВВ1 и СС1 треугольника ABC проведена прямая, паралельная прямой BC и пересекающая стороны AB и AC соответсвено в точках M и N . Докажите, что MN=BM+CN

Answer 1

Треугольник АВС, точка О - пересичение биссектрис ВВ1 и СС1

Треугольники МОС1 и  NОС равнобедренные

Угол ОСВ = углу СОN как внутренние раносторонние при параллельних прямых ВС и МN и секущей СС1 и равен углу  NСО

Угол ОВС = углу ВОМ как внутренние раносторонние при параллельних прямых ВС и МN и секущей ВВ1 и равен углу  ВОМ

  NС = NО, МВ=МО

 NМ= NС+МВ

Answer 2

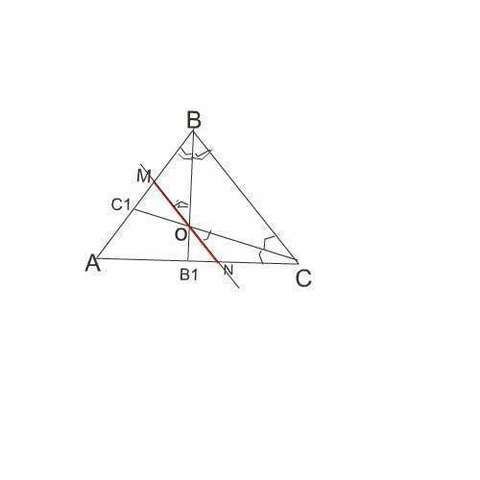
Сделаем рисунок.

Обозначим точку пересечения биссектрис буквой О.
Обратим внимание на две параллельные прямые ВС и МN
Они пересекаются:

1) Секущей ВВ1.

При этом образуются равные накрестлежащие углы СВО и ВОМ по свойству параллельных прямых и секущей.
Но ∠ СВО=∠ВОМ по условию задачи.
Отсюда  ᐃВМО - равнобедренный. МО=МВ

2) Секущей СС1.

При этом образуются равные накрестлежащие углы ВСО и СОN по свойству параллельных прямых и секущей.
Но ∠ОСN=∠ВОС по условию задачи.
ᐃ ОСN - равнобедренный и ОN=NС
Из этого следует, что МО+ОN=ВМ+СN,
иначе МN=ВМ+СN, что и требовалось доказать.

 

---