Начальная скорость:
 мм/с
мм/с  м/с ;
м/с ;
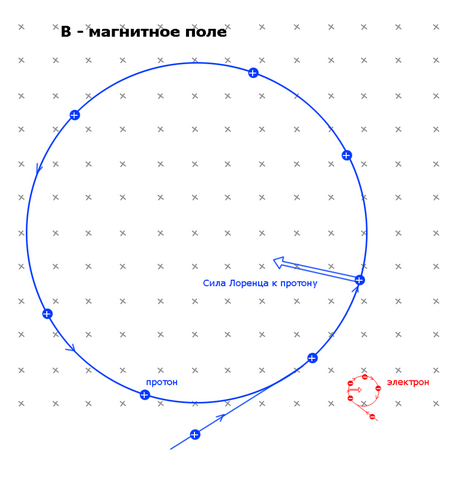
Протон заряжен положительно, а электрон – отрицательно, это означает, что действующая на них сила Лоренца, перпендикулярная к скорости будет направлена в противоположные стороны, по отношению к скорости.
Для определённости, договоримся, что мы считаем, что заданное магнитное поле направлено от нас, т.е. входит в плоскость видимого изображения чертежа.
Сила Лоренца:
 ;
;
В обоих случаях – это будет одна и та же величина, поскольку модули зарядов электрона и протона – равны, и отличаются лишь знаком. Если (для определённости) обе частицы влетают в магнитное поле снизу, то согласно Маховичкам Максвелла, сила Лоренца, действующая на протон, будет направлена по левую руку от вектора скорости и перпендикулярно ему.
Аналогично, сила Лоренца, действующая на электрон, будет направлена по правую руку от вектора скорости и перпендикулярно ему.
Центростремительное ускорение, которое получат частицы:
 ;
;
и
 ;
;
где  и
и  – массы протона и электрона соответственно.
– массы протона и электрона соответственно.
Радиусы вращения частиц в магнитном поле найдём из кинематики вращательного движения:
 ;
;
 ;
;
Итак: радиус вращения протона:
 ;
;
А электрона соответственно:
 ;
;
Длина каждой окружности, это  , значит период обращения частиц:
, значит период обращения частиц:
 ,
,
соответственно для протона это:  ,
,
а для электрона это:  ;
;
Масса протона:  0.001 кг /
0.001 кг /  кг /
кг /  ;
;
 кг.
кг.
Масса электрона:  ;
;
 кг.
кг.
Заряд протона равен заряду электрона  Кл.
Кл.
Значение индукции магнитного поля в задаче не указано, так что для определённости будем считать, что индукция составляет 1 наноТесла, т.е.  нТл
нТл  Тл.
Тл.
Тогда получится, что:
радиус вращения протона:  ;
;
 м
м  мм ;
мм ;
А электрона соответственно:  мм ; в 1837 раз меньше.
мм ; в 1837 раз меньше.
Период обращения протона будет:  ,
,
а для электрона это:  мс ;
мс ;
При увеличения значений индукции магнитного поля, как легко понять – радиусы и периоды будет уменьшаться во столько же раз, и, наоборот, при уменьшении магнитного поля – радиусы и периоды будут увеличиваться во столько же раз.