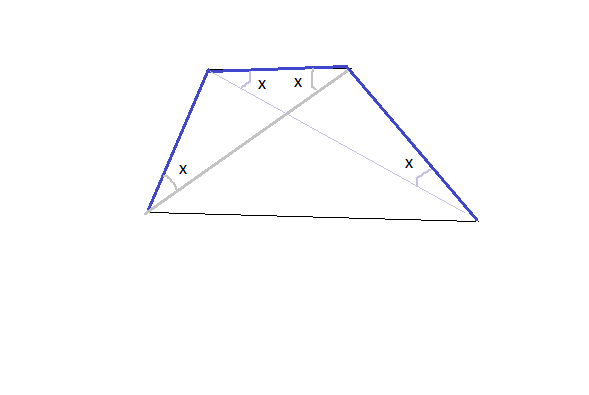
Обозначим отрезки, на которые делит точка касания боковую сторону 4х и 9х
По свойству касательной к окружности, проведенных из одной точки, отрезки касательных равны между собой ( см. на рисунке 1, синие и зеленые отрезки)
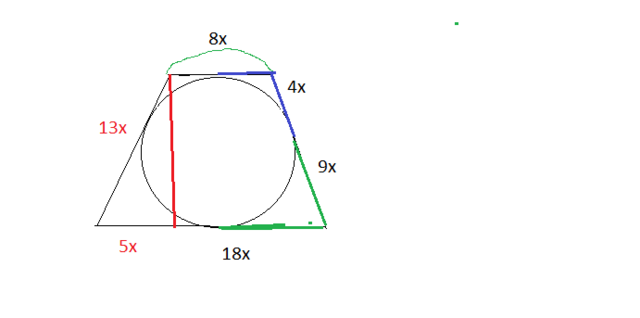
Поэтому верхнее основание 8х, нижнее основание 18х
Проведем высоту из вершины верхнего основания на нижнее, получим прямоугольный треугольник ( см. рисунок 2)
с гипотенузой 13х (боковая сторона)
и катетом 5х( полуразность оснований)
По теореме Пифагора
h²=(13x)²-(5x)²=144x²
h=12x
По условию
h=2r=24 дм
12х=24
х=2
a=8x=8·2=16 дм
b=18x=18·2=36 дм
средняя линия (a+b)/2=(16+36)/2=26 дм