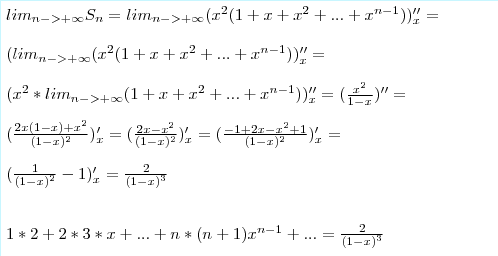Это степенной ряд, найдём его радиус сходимости.
Согласно признаку Даламбера.
+\infty}|\frac{a_n}{a_{n+1}}|= lim_{n -> +\infty}|\frac{(n+1)(n+2)}{(n+2)(n+3)}| =\\\\ lim_{n -> +\infty}|\frac{(n+1)}{(n+3)}| =lim_{n -> +\infty}|1 - \frac{2}{n+3}| = 1 " alt="R = lim_{n -> +\infty}|\frac{a_n}{a_{n+1}}|= lim_{n -> +\infty}|\frac{(n+1)(n+2)}{(n+2)(n+3)}| =\\\\ lim_{n -> +\infty}|\frac{(n+1)}{(n+3)}| =lim_{n -> +\infty}|1 - \frac{2}{n+3}| = 1 " align="absmiddle" class="latex-formula">
Так как радиус сходимости степенного ряда 
равен 1, то при |x| >1, ряд расходится.
Проверим сходимость в точках x = 1 и x = -1.
При x = 1, ряд (*) — расходится (так как не выполняется необходимое условие сходимости числового ряда).
При x = -1, ряд (*) – расходится (так как не выполняется необходимое условие сходимости числового ряда).
Ряд сходится при |x| < 1.
- разложение в ряд Маклорена функции 
См. дальнейшее решение во вложении.
при 
