Помогите . 1)Радиус окружности описанный около квадрата,равен 8 .Найти диагональ квадрата...

Question

51 просмотров

Помогите .
1)Радиус окружности описанный около квадрата,равен 8 .Найти диагональ квадрата .
2)Сторона квадрата равна 18 см.Найти радиус вписанной окружности.
3)Меньшая сторона прямоугольника равна 15 см,острый угол между диагоналями равен 60.Найти радиус окружности описанный около прямоугольника .

Геометрия аноним 13 Апр, 18 | 51 просмотров

Дано ответов: 2

toni77_zn · Answer 1 · 2018-04-12T21:33:15+0000

1) диагональ квадрата=диаметру описанной окружности=8*2=16
2) радиус вписанной окружности равен половине стороны квадрата=18/2=9 см
3) радиус описанной окружности равен половине диагонали прямоугольника и равен меньшей стороне прямоугольника=15 см

аноним · Answer 2 · 2018-04-12T21:33:18+0000

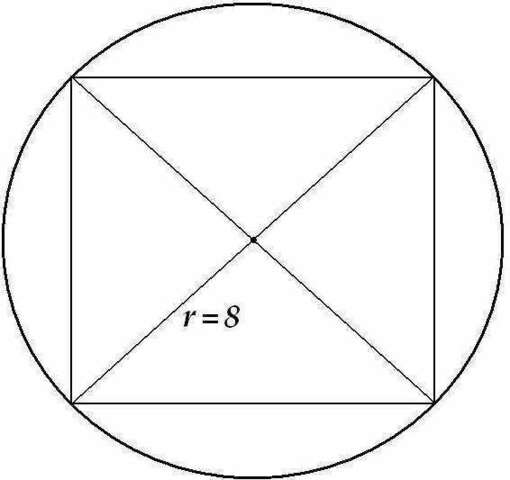
1) В данном случае диагональ квадрата - это и есть диаметр описанной окружности и равен двум радиусам:
$d=2r=2\cdot8=16$

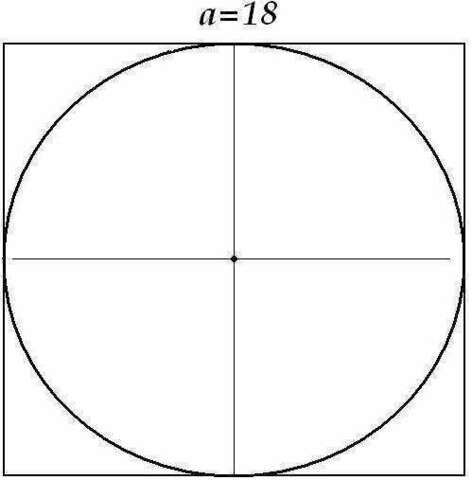
2) В этом случае, наоборот, сторона квадрата - это диаметр вписанной окружности, а радиус равен половине диаметра (или стороны):
$r= \frac{d}{2}=\frac{a}{2}=\frac{18}{2}=9$ см

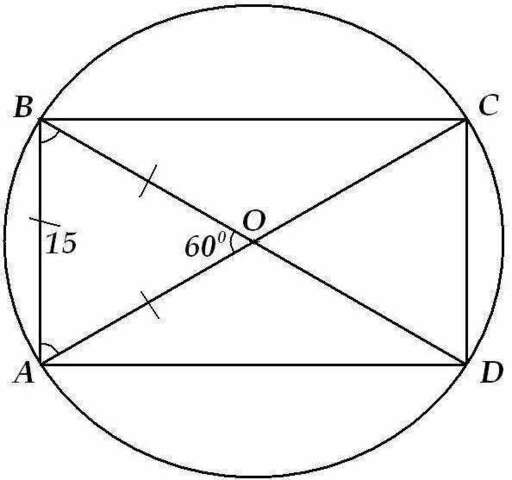
3) Смотрим третий рисунок:
ABCD - прямоугольник, АВ=15, О - точка пересечения диагоналей, ∠АОВ=60°
Известно, что диагонали прямоугольника равны и точкой пересечения делятся пополам, значит АО=ОВ, то есть ΔАОВ - равнобедренный. Но если угол при вершине равен 60°, то и углы при основании равны: $\frac{(180-60)}{2}= \frac{120}{2}=60^0$
Значит ΔАОВ - равносторонний, АО=ОВ=ВС=15 см.
Радиус описанной окружности в данном случае равен половине диагонали, то есть АО или ОВ:
$r=AO=OB=BC=15$ см