Площадь параллелограмма можно вычислить разными способами:
1)
Произведением длины стороны и высоты, проведенной к этой стороне. -Нет значения высоты, но ее можно вычислить.
2)
Произведением трех величин: длин сторон а*b*синус угла между ними. Угол не известен.
3)
Площадь равна половине произведения 2-х диагоналей и синуса угла между ними.
Нет длины второй диагонали и значения угла между ними.
------
Для решения задачи можно воспользоваться первым способом, найдя высоту параллелограмма, проведенную к продолжению АD или CD
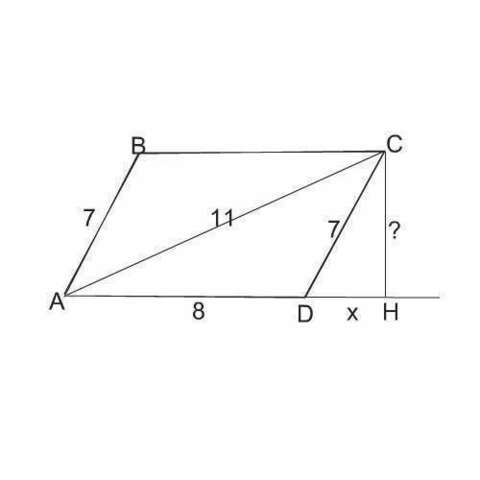
Сделаем рисунок. Проведем высоту к продолжению стороны АD
Высота СН по теореме Пифагора из треугольника
СНD
СН²=СD²-DН²=49-х²
Из треугольника АСН
СН²=АС²-АН²=121-(8+х)²
Так как высота СН одна и та же, приравняем эти уравнения:
49-х²=121 -64-16х-х²
49=121 -64-16х
16х=121-113=8
х=8:16=0,5
Подставим значение х в уравнение высоты
СН² = СD² - DН²=49-0,25
СН=√48,75
S=8·√48,75≈55,85696......
------------------------------------
Проще, на мой взгляд, другой способ.
Диагональю АС параллелограмм поделен на два равных треугольника, стороны которых известны. Площадь параллелограмма равна сумме площадей этих треугольников.
По формуле Герона
................._______________....._________________......_______
Sᐃ АВС= √p(p−a)(p−b)(p−c) = √13(13-7)(13-8)(13-11) = √13*6*5*2 = √780
Площадь параллелограмма в два раза больше
S ABCD = 2·√780≈55,85696......