Как видно, одинаковые задачи в одно время учебного года идут "стаями". Повторяю решение, данное мной день назад.
---------
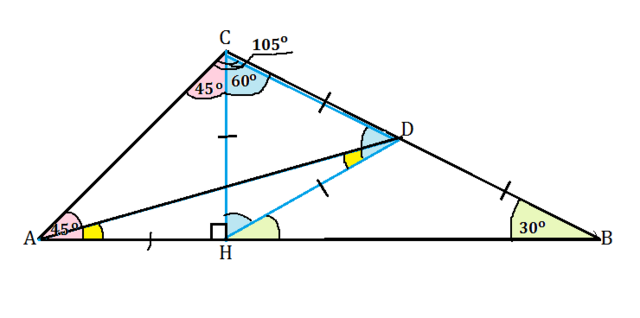
Сделаем рисунок данного треугольника АСВ.
Опустим из С высоту СН на АВ.
Треугольник СНВ - прямоугольный, сумма острых углов прямоугольного треугольника 90°⇒
∠НСВ=60°
Катет СН противолежит углу 30° ⇒
СН=СВ:2 по свойству катета против угла 30°
Так как и СD=СВ:2, СН=СD⇒
треугольник НСD -равнобедренный.
Т.к. угол НСD =60°, а углы при основании НD равны. то
∠СНD=∠СDН=60°
Следовательно, треугольник СНD- равносторонний, НD=СН
Угол АСН=105°-60°=45°
Отсюда ∠ САН=90°-45°=45°
Δ АСН- равнобедренный, АН=СН=НD ⇒
ΔАНD - равнобедренный.
Угол АНD= ∠AHC+∠CHD= 90°+60°=150°
Угол DАН=(180°-150°):2=15° ⇒
Угол ВАD=15°
-------
[email protected]