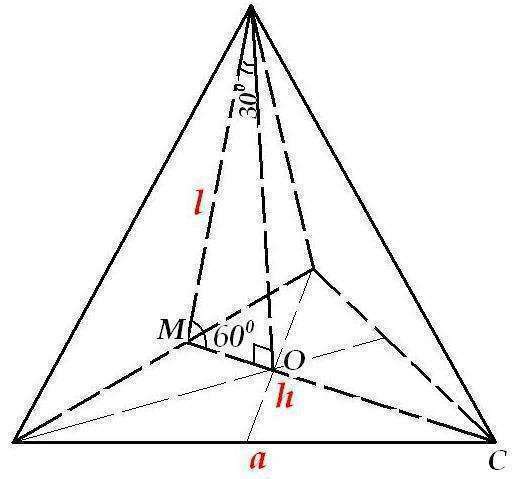
Рисунок без буквенных обозначений (кроме C,O,M), обозначишь, если нужно как угодно, хотя всё понятно и так.
Для удобства и быстроты всей писанины введём буквенные обозначения  -сторона основания,
-сторона основания,  - апофема,
- апофема,  - высота основания. Эти три величины потребуются для всего вычисления.
- высота основания. Эти три величины потребуются для всего вычисления.
МО=3, как катет, лежащий против угла в 30°
Для Δ-ка, лежащего в основании медианы, биссектрисы, высоты совпадают, а точка их пересечения О- является центром основания.
Далее вспоминаем свойство медиан Δ-ка:
Медианы треугольника пересекаются в одной точке, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Поэтому 
Теперь находим  :
:




...Ну и как "Лучший ответ" не забудь отметить, ОК?!.. ;)