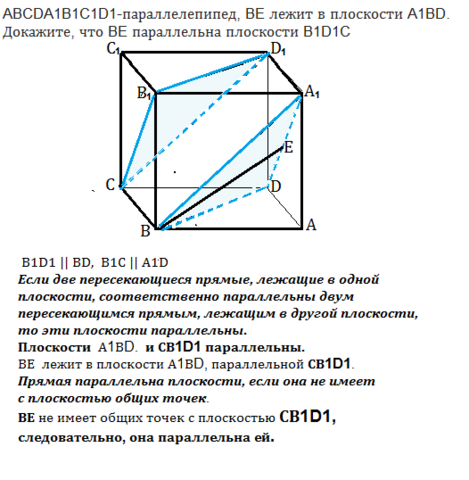
Плоскости А1ВD и В1D1C ограничены равными сторонами треугольников, лежащих на противоположных параллельных сторонах параллелепипеда. В1D1|| BD - лежат в плоскости В1D1DB- равны и параллельны.
CD1||A1B - лежат в плоскости СВА1D1- равны и параллельны
B1C||A1D - лежат в плоскости В1СDA1- равны и параллельны.
Стороны этих треугольников попарно пересекаются друг с другом.
Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости, то эти плоскости параллельны.
Плоскости А1ВD. и СВ1D1 параллельны.
ВЕ лежит в плоскости А1ВD, параллельной СВ1D1.
Прямая параллельна плоскости, если она не имеет с плоскостью общих точек.
ВЕ не имеет общих точек с плоскостью СВ1D1, следовательно, она параллельна ей.