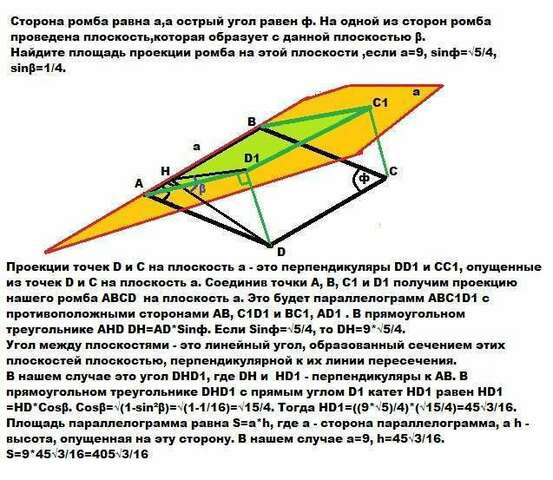
Проекции точек D и С на плоскость а - это перпендикуляры DD1 и СС1, опущенные из точек D и С на плоскость а. Соединив точки А, В, С1 и D1 получим проекцию нашего ромба АВСD на плоскость а. Это будет параллелограмм АВС1D1 с противоположными сторонами АВ, С1D1 и ВС1, АD1 . В прямоугольном треугольнике АНD DH=AD*Sinф. Если Sinф=√5/4, то DН=9*√5/4.
Угол между плоскостями - это линейный угол, образованный сечением этих плоскостей плоскостью, перпендикулярной к их линии пересечения.
В нашем случае это угол DHD1, где DH и HD1 - перпендикуляры к АВ. В прямоугольном треугольнике DHD1 с прямым углом D1 катет HD1 равен HD1=HD*Cosβ. Cosβ=√(1-sin²β)=√(1-1/16)=√15/4. Тогда HD1=((9*√5)/4)*(√15/4)=45√3/16. Площадь параллелограмма равна S=a*h, где а - сторона параллелограмма, а h - высота, опущенная на эту сторону. В нашем случае а=9, h=45√3/16.
S=9*45√3/16=405√3/16