1. Область определения и область значений

2. Четность

Функция не является ни четной, ни нечетной
3. Так как функция непрерывна на

, то вертикальных асимптот нет.

Наклонных асимптот нет
Необходимо выяснить, как ведет себя функция на бесконечности:

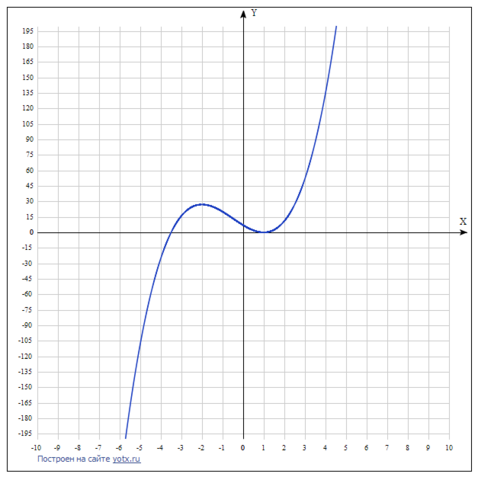
Если идем вправо, то график уходит далеко вверх, если идем влево, то график уходит далеко вниз
4. Нули функции и интервалы
С осью ординат:

C осью абсцисс:


- ниже оси ОХ

- выше оси ОХ
5. Возрастание и убывание функции, экстремумы


- возрастает

- убывает
Подставляем значения в функцию, чтобы определить точки максимума-минимума

В точке А - максимум, в точке В - минимум
6. Выпуклость, вогнутость и точки перегиба


- выпуклость

- вогнутость
Подставляем в функцию:

Точка С - точка перегиба
7. График прилагается