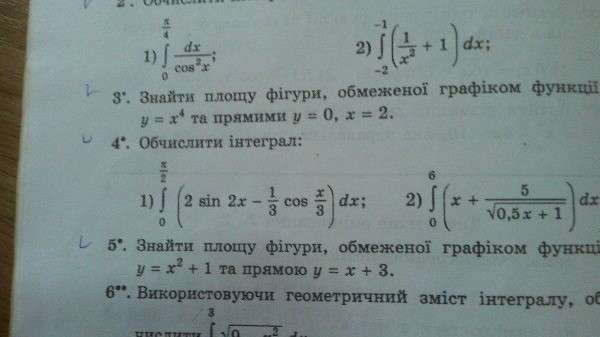Найти площадь фигуры, ограниченной графиком функции y=x^2+1 и прямой y=x+3 (задание...

Question

Найти площадь фигуры, ограниченной графиком функции y=x^2+1 и прямой y=x+3
(задание №5)
Желательно ещё нарисовать график, но я, если что, и сам смогу.


Знайти площу фігури, обмеженої графіком функції y=x^2+1 та прямою y=x+3
(завдання №5)
Бажано намалювати графік, але я, раптом щось, і сам зможу.

---

Comments

Dnepr1, ну хоть вы не передумывайте писать ответ. Умоляю вас!

Answer 1

Так как прямая  у = х + 3 проходит выше нижней части параболы у = х² + 1, то для нахождения площади надо проинтегрировать разность:
(х + 3) - (х² + 1) = -х² + х + 2.
Находим пределы интегрирования, приравняв функции:
х² +1 = х + 3
х² - х - 2 = 0.
Квадратное уравнение, решаем относительно x: 
Ищем дискриминант:D=(-1)^2-4*1*(-2)=1-4*(-2)=1-(-4*2)=1-(-8)=1+8=9;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√9-(-1))/(2*1)=(3-(-1))/2=(3+1)/2=4/2=2;
x_2=(-√9-(-1))/(2*1)=(-3-(-1))/2=(-3+1)/2=-2/2=-1.
Решаем интеграл:
27 / 6 = 9 / 2 = 4.5.
Ответ: S = 4,5.

Comments

Спасибо! Всё так, как я думал. Но вы можете мне объяснить, откуда в решении интеграла взялась двойка, выделенная меня кавычками -1int2(-x^2+x+(((2))))dx? Я просто не могу докумекать, откуда её брать, а ведь мне ещё много таких задач решать придётся.

---

Так вот оно в ответе дано: "Так как прямая у = х + 3 проходит выше нижней части параболы у = х² + 1,то надо проинтегрировать разность: (х + 3) - (х² + 1) = -х² + х + 2".Интеграл даёт площадь от фигуры до оси х. В этом задании площадь заключена между двумя фигурами. Надо из верхней отнять нижнюю.