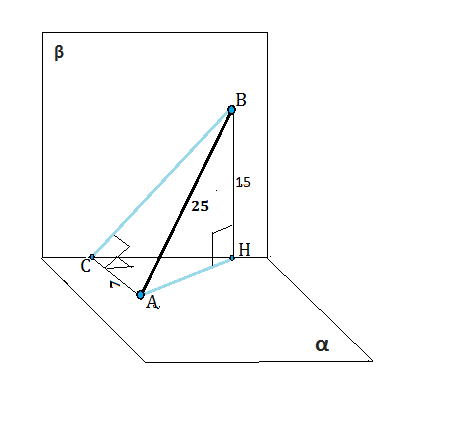
Концы отрезка АВ = 25 см расположены в перпендикулярных плоскостях α и
β и удалены от линии их пересечения соответственно на 15 и 7 см. Найдите длины проекций отрезка АВ на данные плоскости.
-----------
Расстояние от точки до прямой - длина перпендикуляра, проведенного из этой точки к прямой.
Пусть точка А лежит в плоскости α, а точка В в плоскости β.
Тогда АС=15 см, а ВН=7 см.
Проекция АВ на плоскость α равна длине отрезка АН.
АН - наклонная к плоскости β. СН - ее проекция на плоскость β.
ВН ⊥ СН как расстояние от В до СН.
По т. о трех перпендикулярах прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.
Треугольник АВН прямоугольный. Отношение катета ВН к гипотенузе АВ равно 3:5, и этот треугольник -
египетский.
Значит,
АН=20 ( можно проверить по т.Пифагора).
ВС - наклонная к плоскости α , СН ее проекция на плоскость α, и по т. о трех перпендикулярах ВС ⊥ АС, треугольник АВС прямоугольный. Отношение катета АС к гипотенузе ВС равно 7:25.
Этот треугольник из так называемых
троек Пифагора, и
ВС=24 см ( можно проверить по т.Пифагора).
Длины проекций отрезка АВ на данные плоскости. равны
20 см на плоскость α и 24 см на плоскость β.