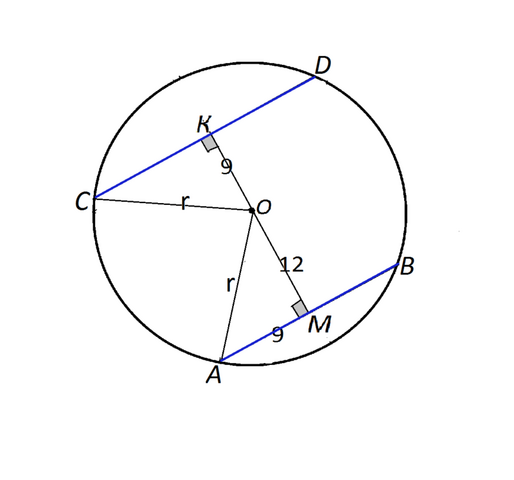
Сделаем рисунок.
Можно хорды нарисовать параллельными, т.к. расстояние от центра окружности до хорд и радиус заданы условием, поэтому, поэтому длина хорд не меняется от места их расположения.
Расстояние от точки до прямой измеряют отрезком, перпендикулярным к ней. ⇒
углы СКО и АМО - прямые, а треугольники СКО и АМО - прямоугольные. Радиус окружности является их гипотенузой, а половина АВ=9 .
Из треугольника АМО найдем радиус r.
Треугольник - египетский, т.к. отношение катетов 3:4, следовательно, радус равен 15 ( можно проверить по т. Пифагора).
Треугольники СКО и АМО равны по гипотенузе и меньшему катету, из чего следует, что больший катет второго треугольника равен 12.
СD=2 СК=24.
-------
bzs*