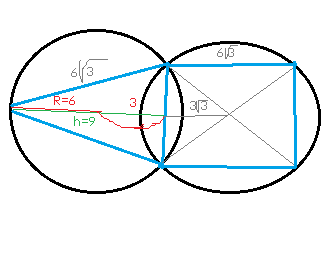
См. рисунок и решение на рисунке
Высота равностороннего треугольника
h=6√3·cos 30°=6√3·√3/2=9 cм

d=h-R=3 cм - расстояние от центра окружности, в которую вписан треугольник до данной хорды
Расстояние от центра окружности, в которую вписан квадрат, до данной хорды равно половине стороны квадрата
Ответ. 3+3√3 ( см)