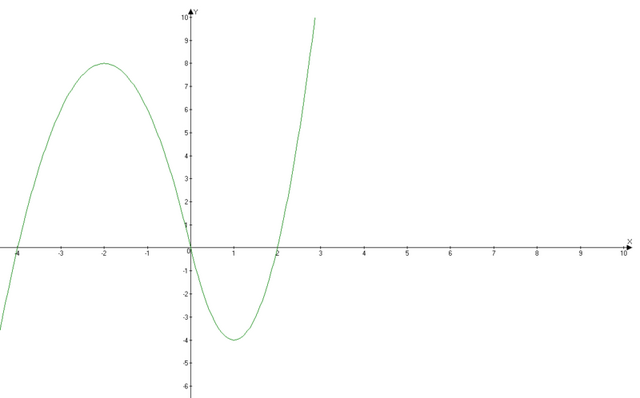
Рассмотрим функции
f(x) = 3x*|x| + x² - 8x и g(x) = c
f(x) = 3x*|x| + x² - 8x
Если x>0, то f(x) = 3x² + x² - 8x = 4x² - 8x
m=-b/2a = 8/8 = 1
f(1) = 4-8 = -4
(1;-4) - координаты вершины параболы
Если x<0, то f(x) = -3x² + x² - 8x = -2x² - 8x<br>m=-b/2a = 8 / (-4) = -2
f(-2) = -2 * (-2)² - 8 * (-2) = 8
(-2;8) - координаты вершины параболы
График смотрите в приложении.
g(x) = c - прямая, параллельная оси Ох
Видим что c=±8 пересечений с графиком f(x) и g(x) будет 2, а значит уравнение имеет 2 корня
Ответ: при c = ±8