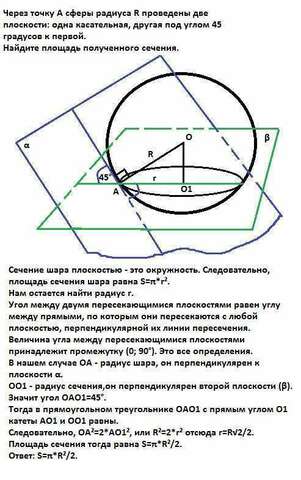
Сечение шара плоскостью - это окружность. Следовательно, площадь сечения шара равна S=π*r². Нам остается найти радиус r.
Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения.
Величина угла между пересекающимися плоскостями принадлежит промежутку (0; 90°). Это все определения.
В нашем случае ОА - радиус шара, он перпендикулярен к плоскости α.
ОО1 - радиус сечения,он перпендикулярен второй плоскости (β).
Значит угол ОАО1=45°.
Тогда в прямоугольном треугольнике ОАО1 с прямым углом О1 катеты АО1 и ОО1 равны.
Следовательно, ОА²=2*АО1², или R²=2*r² отсюда r=R√2/2.
Площадь сечения тогда равна S=π*R²/2.
Ответ: S=π*R²/2.