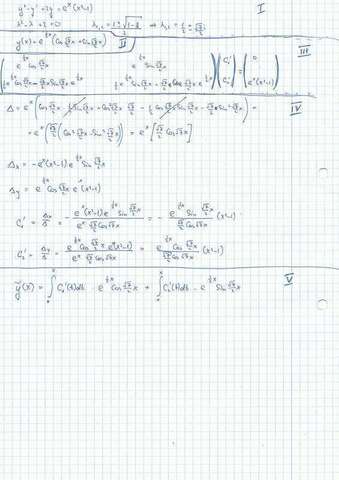Решение в приложении.
Комментарии к решению:
Часть I
Решаю однородное уравнение для нахождения базис-векторов пространства решений уравнения.  здесь - собственные числа, а
здесь - собственные числа, а
 - базис пространства решений уравнения.
- базис пространства решений уравнения.
Помним, что решение неоднородной системы есть функциональная комбинация векторов базиса:
 .
.
Часть III
Определяю матрицу Вронского (Вронскиан).
Теперь нужно решить систему уравнений, где вектор-неизвестное  - это подходящие функции для функциональной комбинации.
- это подходящие функции для функциональной комбинации.
Часть IV
Решение системы.
Способ решения может быть любой, я использовал метод Крамера.
Часть V
Проинтегрировав функции (чего я не сделал), получаем множество решений уравнения  - функциональную комбинацию (для нахождения решения, выполняющего начальные условия, нужно проинтегрировать
- функциональную комбинацию (для нахождения решения, выполняющего начальные условия, нужно проинтегрировать  и подставить начальные условия для нахождения свободного коэффициента получаемого при интеграции).
и подставить начальные условия для нахождения свободного коэффициента получаемого при интеграции).
P.S. метод попроще я, увы, не нашёл: все известные мне "хитрые подстановки" в частное решение, при комплексных лямбдах  , ограничиваются
, ограничиваются  . Что подставлять для
. Что подставлять для  - без понятия.
- без понятия.