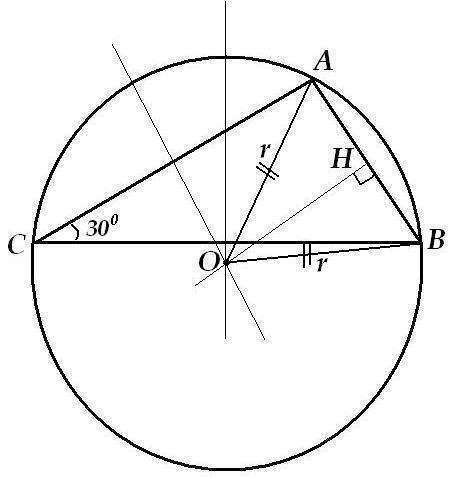
Пусть О - центр окружности, описанной около ΔАВС.
Рассмотрим ΔАОВ:
ОА=ОС=r, значит ΔАОВ -равнобедренный (впоследствии он окажется и равносторонним, но это при решении данной задачи значения не имеет). Точка Н- середина стороны АВ, через неё проведён серединный перпендикуляр ОН, который является медианой, биссектрисой и высотой.
Так как
Н- середина стороны АВ, то АН=НВ=120.
∠АСВ=30° является вписанным углом, опирающимся на дугу АВ, значит градусная мера дуги АВ=60°
∠АОВ при этом является центральным углом, опирающимся на дугу АВ, значит ∠АОВ=60°
Рассмотрим Δ ОНВ: он прямоугольный, т.к. ОН⊥АВ; ∠НОВ=30°, т.к. ОН является и биссектрисой; а НВ=120 это катет, лежащий против угла в 30°.
Значит

...Ну и как "Лучший ответ" не забудь отметить, ОК?!.. ;)