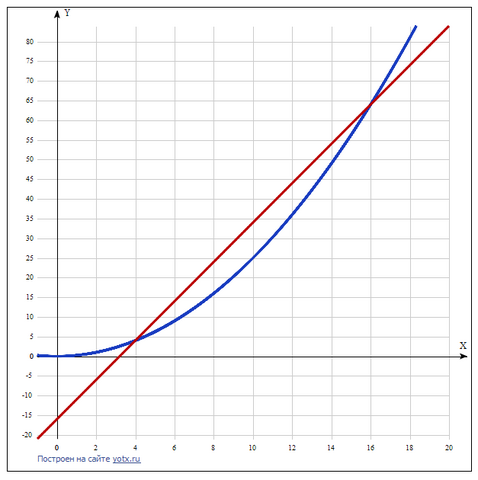
Если графики пересекаются, у них есть общие точки. То есть надо приравнять функции:
(1/4)х² = 5х - 16.
(1/4)х² - 5х + 16 = 0.
Решаем уравнение 0.25*x^2-5*x+16=0:
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-5)^2-4*0.25*16=25-4*0.25*16=25-16=9;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(2root9-(-5))/(2*0.25)=(3-(-5))/(2*0.25)=(3+5)/(2*0.25)=8/(2*0.25)=8/0.5=16;
x_2=(-2root9-(-5))/(2*0.25)=(-3-(-5))/(2*0.25)=(-3+5)/(2*0.25)=2/(2*0.25)=2/0.5=4.
Есть 2 точки пересечения:
х1 = 4 у1 = 5*4 - 16 = 20 - 16 = 4.
х2 = 16 у2 = 5*16 - 16 = 80 - 16 = 64.