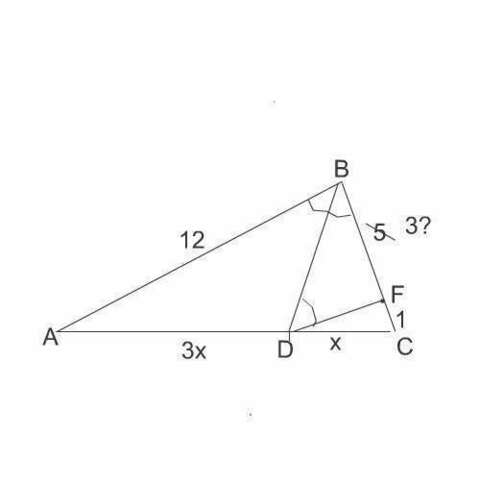
Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон, есть у нее такое свойство.
Т.е. АD:DС=АВ:ВС
Думаю, доказать, что FD|| АВ, вряд ли кто-то сумеет при данных в условии задачи отношениях отрезков на АС и ВС.
Поясню подробно.
FD может быть параллельно АВ в том случае, если треугольники АВС и FDС подобны.
Тогда углы АВD и ВDF равны как накрестлежащие,
углы ВDFи DВF равны как углы, равные половине угла В, и
FD равна ВF как сторона равнобедренного треугольника с равными углами при основании ВD.
И АС:DС=ВС:СF
Но по условию задачи
АС:DС=4:1,
а ВС:СF=6:1 - не получается ни подобия, ни применения свойства биссектрисы треугольника.
Поэтому здесь возможны два варианта:
1) либо задача специально дана с заведомо неверными величинами для того, чтобы решающий ее доказал невозможность FD|| АВ
2) либо условие задачи по ошибке списано неверно.
--------------
НО если сторона ВС равна 4, все получится.
Тогда FD=3 см как соответственная сторона стороне АВ при отношении сторон 4:1, так и из равнобедренного треугольника ВDF, где DF=ВF=3 см
И отношения отрезков основания АС будут равны отношению АВ:ВС,
и АС:DС=4:1,
а ВС:СF=4:1