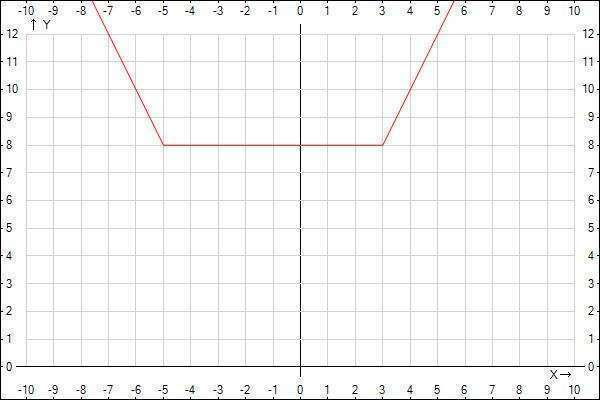
Побудуємо графік функції y=|x+5|+|x-3| (див. в вкладиші)
Графік правої частини : графік y=a - пряма паралельна осі абсцис.
Розвязки рівнняння - це абсциси точок перетину графіків y=|x+5|+|x-3| і y=a
При a>8 два розвязки
При а=8 безліч розвязків а саме будь-яке число з відрізка [-5;3]
При a<8 розвяків немає</strong>
y=|x+5|+|x-3|
при x>=3 має вигляд y=x+5+x-3=2x+2
y=2x+2
при -5<=x<3 має вигляд y=x+5-x+3=8</p>
y=8
при x<-5 має вигляд y=-x-5-x+3=-2x-2</p>
y=-2x-2