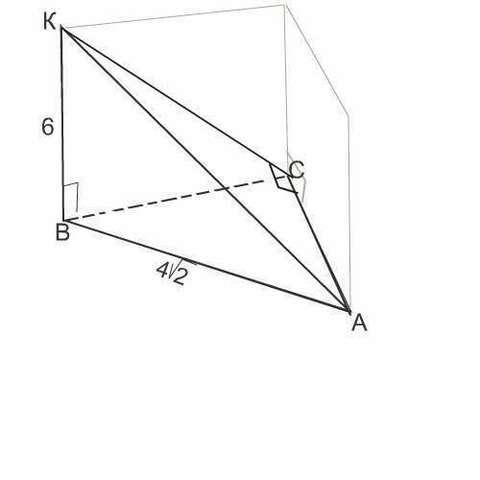
Треугольник АКС прямоугольный по теореме о трех перпендикулярах:
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.
Проекция наклонной КС - катет ВС прямоугольного треугольника АВС с прямым углом С.
Угол КСА=90°
Чтобы найти площадь ⊿АКС, надо найти длину его катетов КС и СА.
СА - катет равнобедренного прямоугольного треугольника АСВ.
Гипотенуза АВ=4√2, следовательно, АС=ВС=4( по формуле диагонали квадрата
d=а√2, т.к. АСВ - половина квадрата с диагональю АВ) и а=4
Можно найти катеты и по теореме Пифагора с тем же результатом.
КС найдем по теореме Пифагора из треугольника КВС
КС²= КВ²+ВС² =36+16=50
КС=5√2
S ⊿АКС =4*5√2=20√2
------------
Перпендикулярными являются плоскости треугольников КВС и АВС