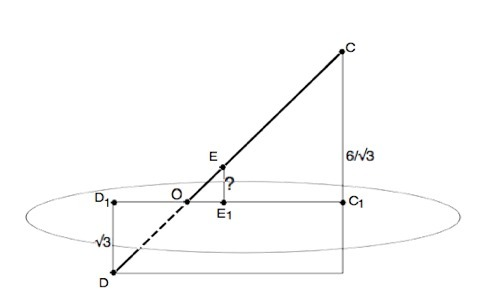
Обозначим точку пересечения плоскости β отрезком CD буквой О.
DD1║CC1, CD- секущая, ⇒ накрестлежащие ∠D=∠C, вертикальные углы при О равны, ⇒ ∆ DOD1 подобен ∆ COC1 по первому признаку.
k=CC1:DD1=6/√3:√3=2
Тогда СО=2DO=²/₃ СD
ЕО=СО-СЕ

∆ COC1 подобен ∆ EOE1 по первому признаку подобия ( ∠С=∠Е - соответственные при пересечении параллельных прямых ЕЕ1 и СС1 секущей CD, угол О - общий).
 ⇒
⇒