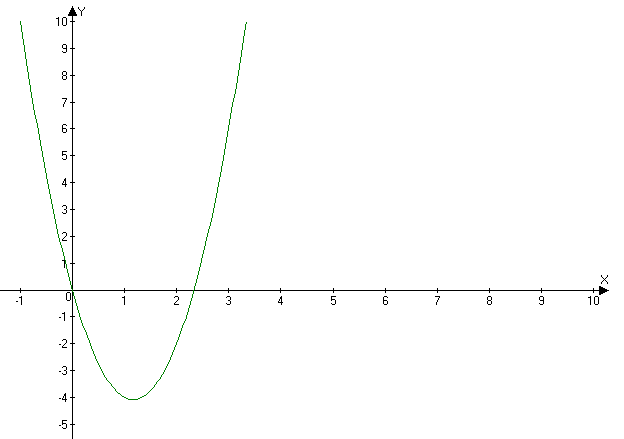Квадратичной функцией называется функция вида:
y=a*(x^2)+b*x+c,
где а – коэффициент при старшей степени неизвестной х,
b – коэффициент при неизвестной х,
а с - свободный член.
Графиком квадратичной функции является кривая, называемая параболой.
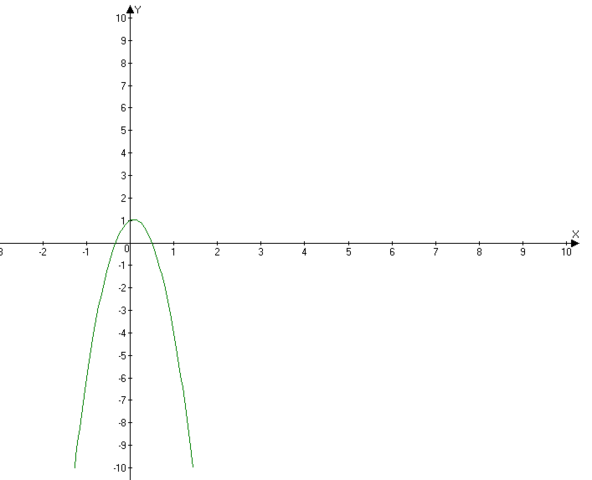
График первый!)

В данном случае у нас ветви направлены вниз.
1) Область определения функции: Множество всех действительных чисел, тоесть: D(y) = R
2) Найдём координату вершины параболы

Найдём значение функции в точке х=1/12

Так как ветви направлены вниз, то область значения функции будет  , тоесть:
, тоесть: ![E(y)=(-\infty;\frac{25}{24}] E(y)=(-\infty;\frac{25}{24}]](https://tex.z-dn.net/?f=E%28y%29%3D%28-%5Cinfty%3B%5Cfrac%7B25%7D%7B24%7D%5D)
Наибольшее значение функции y=25/24, а наименьшей - нет!
Функция возрастает на промежутке  , а убывает на промежутке
, а убывает на промежутке 
Второй график!)

В данном случае у нас ветви направлены вверх.
1) Область определения функции: Множество всех действительных чисел, тоесть: D(y) = R
2) Найдём координату вершины параболы

Найдём значение функции в точке х=7/6

Так как ветви направлены вверх, то область значения функции будет  , тоесть:
, тоесть: 
Наименьшее значение функции x=-49/12, а наибольшего нет.
Функция возрастает на промежутке  , а убывает на промежутке
, а убывает на промежутке 
Если Вам помог, будьте добры, поблагодарите профиль!)