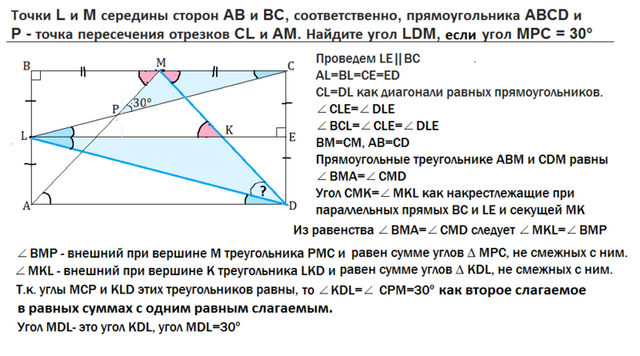
Проведем LЕ||ВСAL=ВL=СЕ=ЕDСL=DL как диагонали равных прямоугольников.
∠СLЕ=∠DLЕ∠ВСL=∠СLE=∠DLЕ
ВМ=СМ, АВ=СD
Прямоугольные треугольнике АВМ и СDМ равны
∠ВМА=∠СМD
Угол СМК=∠МКL как накрестлежащие при параллельных прямых ВС и LЕ и секущей МК
Из равенства ∠ВМА=∠СМD следует ∠МКL=∠ВМР
∠ВМР - внешний угол при вершине М треугольника РМС и равен сумме углов ∆ МРС, не смежных с ним.
∠МКL - внешний угол при вершине К треугольника LКD и равен сумме углов ∆ КDL, не смежных с ним.
Т.к. углы МСР и КLD этих треугольников равны, то ∠ КDL=∠ СРМ=30º
Угол МDL- это угол КDL, угол МDL=30º
---------
Вариант решения.
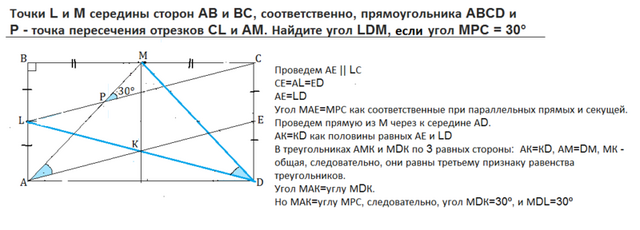
Проведем АЕ || LС
СЕ=АL=ЕD
АЕ=LD
Угол МАЕ=МРС как соответственные при параллельных прямых и секущей.
Проведем прямую из М через к середине АD. АК=КD как половины равных АЕ и LD
В треугольниках АМК и МDК по 3 равных стороны: АК=КD, АМ=DМ, МК - общая, следовательно, они равны третьему признаку равенства треугольников. Угол МАК=углу МDК.
Но МАК=углу МРС, следовательно, угол МDК=30º, и МDL=30º