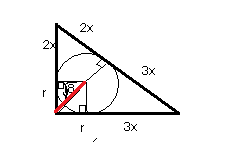См обозначения и рисунок в приложении
По свойству касательных, проведенных к окружности из одной точки, отрезки касательных равны.
По теореме Пифагора
r²+r²=(√8)²
2r²=8
r²=4
r=2
По теореме Пифагора
(2х+2)²+(3х+2)²=(5х)²
4х²+8х+4+9х²+12х+4=25х²
12х²-20х-8=0
3х²-5х-2=0
D=25+24=49
x=2 или х=-1/3 не удовл условию
2·2+2=6 -длина одного катета
3·2+2=8 - длина другого катета
5·2=10 - длина гипотенузы
Р=6+8+10=24
Ответ. 24