1) Производная функции у= (12-3х)*e^(x+100) равна -3e^(x+100)*(x-3).
Максимум находим при производной, равной 0.
умах = 3*e^(103) при х = 3.
2) Производная функции у= 2х / (x²+1) равна -2(x²-1) / ((x²+1)²).
Максимум находим при производной, равной 0.
Для дроби нулю приравнять достаточно числитель:
-2(x²-1) = 0
x² = 1
х = +-1.
Максимум при х = 1.
3) Производная функции равна коэффициенту при х уравненмя касательной.
3x²-15x+12 = -6
Получаем квадратное уравнение:
3х²-15х+18=0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-15)^2-4*3*18=225-4*3*18=225-12*18=225-216=9;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√9-(-15))/(2*3)=(3-(-15))/(2*3)=(3+15)/(2*3)=18/(2*3)=18/6=3;
x₂=(-√9-(-15))/(2*3)=(-3-(-15))/(2*3)=(-3+15)/(2*3)=12/(2*3)=12/6=2.
Проверив значения у при полученных значениях х, определяем, что общая точка имеется только при х = 2.
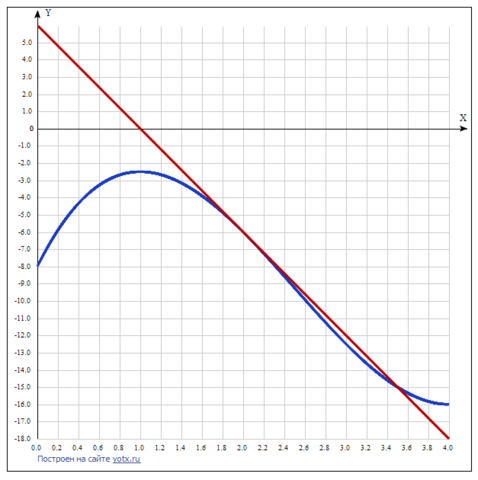
График этой функции прилагается.