Докажите, что сумма радиусов вписанной и описанной окружностей в прямоугольном...

Question

Докажите, что сумма радиусов
вписанной и описанной окружностей в
прямоугольном треугольнике равна
полусумме катетов.

Answer 1

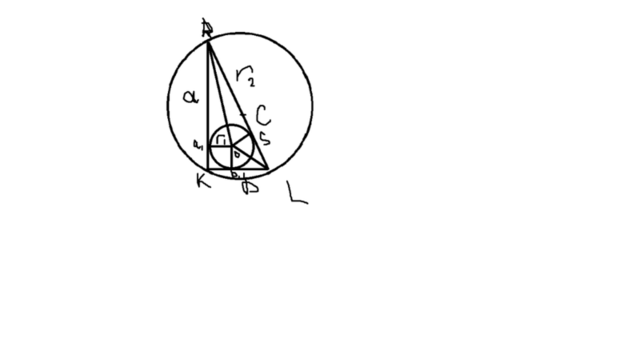
Пусть а,b-катеты, с-гипотенуза, тогда r2(радиус описанной окружности)=с/2
r1=(a+b-c)/2
Докажем , что r1=(a+b-c)/2
Проведем касательные к катетам, a1ob1k-квадрат, со стороной равной r1
тогда a1R=a-r1, b1L=b-r1
ΔRa1o=ΔRoS,Δob1L=ΔSol по катету и гипотенузе⇒
с=a-r1+b-r1, 2r1=a+b-c,r1=(a+b-c)/2
r1+r2=(a+b-c)/2+c/2=(a+b+c-c)/2=(a+b)/2
ч.т.д.

---