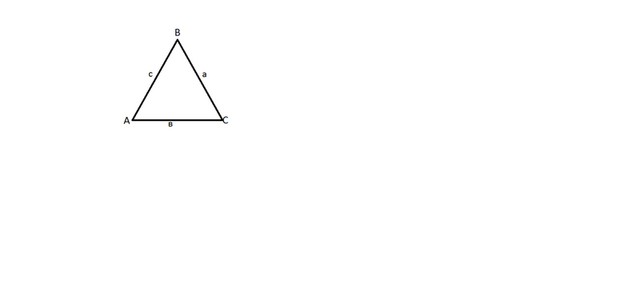Сроочно!!Ребятки,всем доброго времени суток!Помогите,пожалуйста,по алгебре:)
Дано: треугольник АВС. сторона а=97,сторона в=23√3,∠С=150°
получается надо найти: сторону с,и углы А и В т.е. решить треугольник.так-то там через косинус.для меня это дремучий лес.