В правильном треугольной пирамиде SABC боковое ребром SA=6, а сторона основания AB=4....

Question

В правильном треугольной пирамиде SABC боковое ребром SA=6, а сторона основания AB=4. Найдите площадь сечения пирамиды плоскостью, проходящей через ребро AB перпендикулярно ребру SC. Можно с чертежом

Answer 1

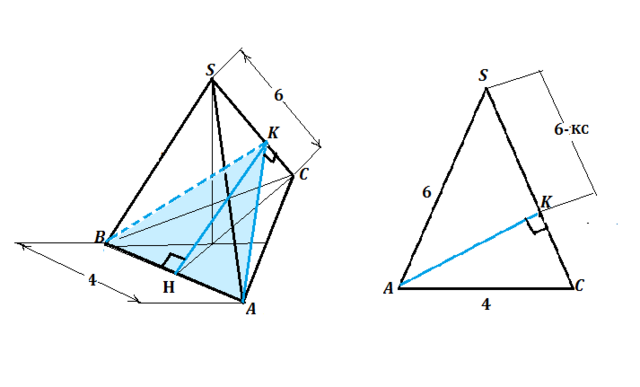
Искомая площадь - это площадь треугольника АВК, где К- основание перпендикуляров АК, ВЕ  к ребру SC и. плоскость этого треугольника -сечение, перпендикулярное ребру SC.
Площадь треугольника равна половине произведения его высоты на основание.
 Основание АВ=4, высоту КН нужно найти. 
КН=√(AK²-АН²) 
АК-катет прямоугольных треугольников АКС и АКS 
Выразим его квадрат из каждого треугольника и приравняем выражения.
АК²=АС²-КС²=16-КС² 
АК²=(СS-КС)²=36-36 +12 КС-КС²= 12 КС-КС²
16-КС²=12 КС-КС²⇒
12 КС=16 
КС=16:12=4/3 
Из треугольника АКС 
АК²=16-16/9=128/9 
Найдем высоту треугольника АВК по т. Пифагора:
КН²=AK²-KC²=128/9-4=92/9 
КН=√(92/9)=2/3*(√23) 
S∆ АВК=2/3*(√23)*4:2=4/3*(√23) (ед. площади)

---

Comments

Не приведен обоснование построения сечения, а вычисления BK можно проще : S(ΔBSC) =SC*BK/2 ⇒BK =2S(ΔBSC)/SC ;площадь Δ _ по формуле Герона или использованием его равнобедренность. Чертеж _ выглядит прекрасно