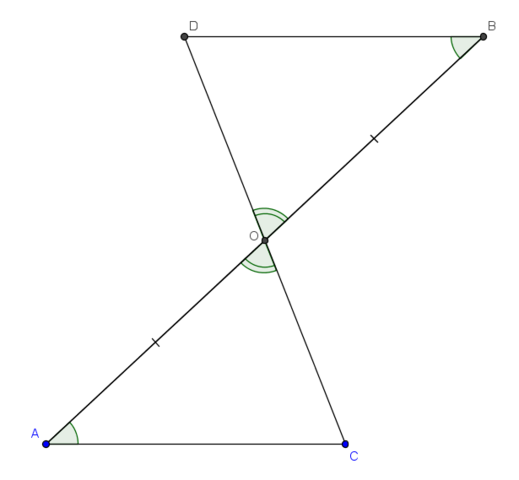
5. Треугольники OAC и OBD равны по стороне и двум углам (AO = OB и ∠OAC = ∠OBD по условию, AOC = BOD потому что вертикальные). Поэтому угол ACO равен углу ODB, т.е. ∠ACO = 63°.
Можно показать, что на самом деле условие равенства AO и OB лишнее: например, прямые AC и BD параллельны (так как их накрест лежащие углы равны), из чего следует равенство ∠ACO = ∠ADB.
6. Можно воспользоваться заклинанием "против равных углов лежат равные стороны" (на самом деле, эта теорема доказывалась применительно к одному треугольнику, но раз тут треугольники равные, то их можно совместить при наложении, т.е. на самом деле это один и тот же треугольник). Итак, против равных углов BAO и DCO лежат равные стороны BO и OD, значит, O делит BD в отношении BO : OD = 1 : 1.