87.
1)
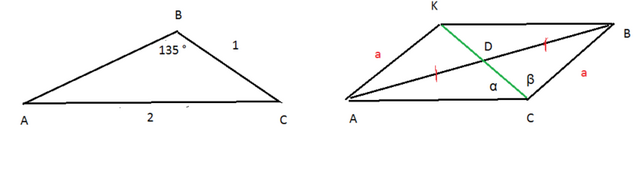
см. рисунок
По теореме синусов:
АС: sin ∠B=ВС: sin ∠ A
sin ∠ A= BC·sin∠B : AC=√2/4.
Ответ.sin ∠ A= √2/4.
107.
см. рисунок
Продолжим медиану CD на длину DK.
Получим параллелограмм АКВС.
∠ВКС=∠АСК=α
Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
∠КВС=180°-α-β
По теореме синусов из треугольника КВС:
ВС: sin ∠ ВКС=КС: sin ∠ КВС
а : sin (180°-α-β)=КС : sin α
sin (180°-α-β)= sin (α+β)
КС= 2СD=a·sinα / sin(α+β) ⇒ CD=a·sinα /2· sin(α+β)
Ответ. CD=a·sinα /2· sin(α+β)