Подобие треугольников --- это "про равные углы"...
в треугольнике АВС больший угол (против большей стороны) ∠АВС
в ΔКАС самая длинная сторона (против большего угла)-- сторона КС
в любом случае КС пропорциональна АС: KC = k*AC = 10k
вторая сторона ΔКАС АС=10
осталось определиться с третьей стороной (АК)
возможны два варианта:
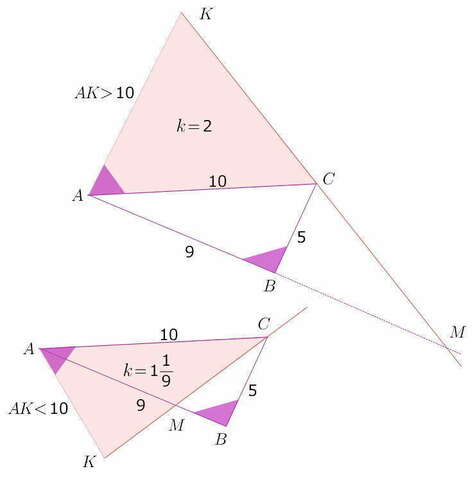
АК > AC или AK < AC
1) AK > 10
тогда АС самая короткая сторона ΔКАС и она пропорциональна ВС
АС = k*BC ---> 5k = 10 ---> k = 2
тогда КС = 20, АК = k*9 = 18
по т.косинусов 10² = 20² + 18² - 2*20*18*cos(AKC)
cos(AKC) = (400+324-100) / (40*18) = 624/(4*6*30) = 26/30 = 13/15
2) AK < 10
тогда АK самая короткая сторона ΔКАС и она пропорциональна ВС
АK = k*BC = 5k, а АС пропорциональна средней стороне АВ
АС = k*АВ ---> k = 10/9
тогда КС = 100/9, АК = 50/9
по т.косинусов 10² = (100/9)² + (50/9)² - 2*100*50*cos(AKC) / 81
100*81 = 100*100 + 25*100 - 100*100*cos(AKC)
cos(AKC) = (100+25-81) / 100 = 44/100 = 0.44
--------------------------------------------------------------------
другими словами, можно было просто посчитать косинусы оставшихся двух углов ΔАВС --- ∠САВ и ∠АСВ, но важно понимать---почему...
а по косинусу ∠АВС (бО'льшего угла треугольника)) и
по т.косинусов можно определить вид треугольника АВС (и КАС)))
10² = 9² + 5² - 2*9*5*cos(ABC)
cos(ABC) = (81+25-100) / 90 = 6/90 = 1/15 > 0 ---> треугольник остроугольный))