Дана функция:
y=(x-5)² *e^x-7
найдем производную:
y'=2(x-5)*e^x-7 +(x+5)² *e^x-7
приравняем к нулю:
2(x-5)*e^x-7 +(x+5)² *e^x-7 =0 (разделим на e^x-7)
2x-10+x²-10x+25=0
x²-8x+15=0
Д=64-4*1*15=64-60=4 (2)
x1=8+2/2=5
x2=8-2/2=3
........
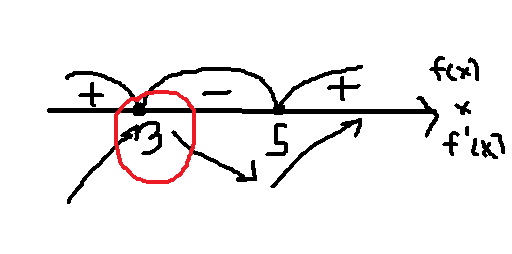
(рисунок)
........
Ответ: 3