Решите систему уравнений графическим методом и методом подстановки:

Question

Дан 1 ответ

almazeratti_zn · Answer 1 · 2018-04-06T23:11:34+0000

$\left \{ {{x-2y=3} \atop {x+y=4}} \right.$
Начнём с метода подстановки:
Выберем одну переменную из двух (пусть будет x) и уравнение (пусть будет первое), и перегоним всё остальное в правую часть; второе перепишем без изменений:
$\left \{ {{x=3+2y} \atop {x+y=4}} \right.$
Далее возьмём правую часть из первого уравнения (3+2у) и подставим её в х второго уравнения:
$\left \{ {{x=3+2y} \atop {3+2y+y=4}} \right. \left \{ {{x=3+2y} \atop {3y=1}} \right.$
Найдём у из второго уравнения (решаем как обычно):
$\left \{ {{x=3+2y} \atop {y= \frac{1}{3} }} \right.$
Мы получили значение у ( $y= \frac{1}{3}$ ). Теперь подставим то самое значение в у первого уравнения:
$\left \{ {{x=3+2* \frac{1}{3} } \atop {y= \frac{1}{3} }} \right.$
Решаем первую часть системы как обычное уравнение (оно и есть обычное):
$\left \{ {{x=3+\frac{2}{3} } \atop {y= \frac{1}{3} }} \right. \left \{ {{x=3 \frac{2}{3} } \atop {y= \frac{1}{3} }} \right.$

Вот мы получили ответ: $x= 3\frac{2}{3} ; y= \frac{1}{3}$

Теперь графический:
Выразим из второго уравнения системы y:
$x+y=4 \\ y=4-x$
Построим функцию у=4-х;
После выразим у из первого уравнения системы:
$x-2y=3 \\ -2y=3-x \\ 2y=-3+x \\ 2y=x-3 \\ y= \frac{x-3}{2}$
Построим функцию $y= \frac{x-3}{2}$ ; Можно записать вторую функцию более красиво: $y= \frac{x-3}{2} = \frac{x}{2} - \frac{3}{2} = 0,5x-1,5$
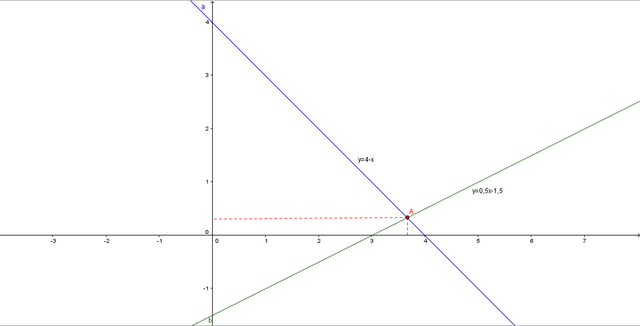
На картинке ниже синим отмечена прямая y=4-x; зелёным - прямая у=0,5х-1,5
Вы же строите прямые вручную по точкам (ну или если совсем лень - перерисовываете), и находите точку пересечения прямых (у меня точка А, обозначена красным). Далее находите координаты этой точки (у меня пунктирным красным).
Эти самые координаты и будут ответами. Для х: координата х, для у - координата у. Вот и всё.
Графический способ подтвердил метод подстановки:
Ответы: $x= 3\frac{2}{3}; y= \frac{1}{3}$