Решение выполняется в предположении, что пятиугольник выпуклый и это предполагается без проверки.
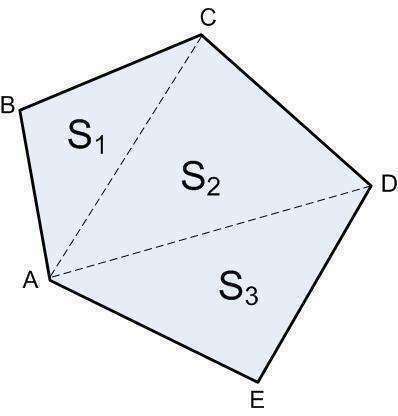
Рассмотрим выпуклый пятиугольник ABCDE, приведенный во вложении. Проведя из вершины А лучи в вершины C и D, разобьем пятиугольник на три треугольника. Тогда можно утверждать, что площадь такого пятиугольника будет складываться из площадей трех полученных треугольников, т.е.
S=S₁+S₂+S₃
Пусть точка А имеет координаты (x₁;y₁), точка B - координаты (x₂;y₂) и точка C - координаты (x₃;y₃). Тогда площадь ΔABC=S₁ можно найти по формуле:

Аналогично, для площадей S₂ и S₃ запишем

//PascalABC.Net 3.0, сборка 1052
type
Point=record
x,y:double
end;
function TriangleSquare(A,B,C:Point):double;
begin
Result:=0.5*abs(A.x*(B.y-C.y)+B.x*(C.y-A.y)+C.x*(A.y-B.y))
end;
procedure GetPoint(c:char; var A:Point);
begin
Write('Введите координаты точки ',c,': ');
Readln(A.x,A.y)
end;
var
A:array['A'..'E'] of Point;
i:'A'..'E';
s1,s2,s3,s:double;
begin
for i:='A' to 'E' do GetPoint(i,A[i]);
s1:=TriangleSquare(A['A'],A['B'],A['C']);
s2:=TriangleSquare(A['A'],A['C'],A['D']);
s3:=TriangleSquare(A['A'],A['D'],A['E']);
s:=s1+s2+s3;
Writeln('Площадь пятиугольника равна ',s:0:2);
end.
Тестовое решение:
Введите координаты точки A: -5 2
Введите координаты точки B: -1 4
Введите координаты точки C: 2 2
Введите координаты точки D: 1 0
Введите координаты точки E: -3 0.5
Площадь пятиугольника равна 16.50