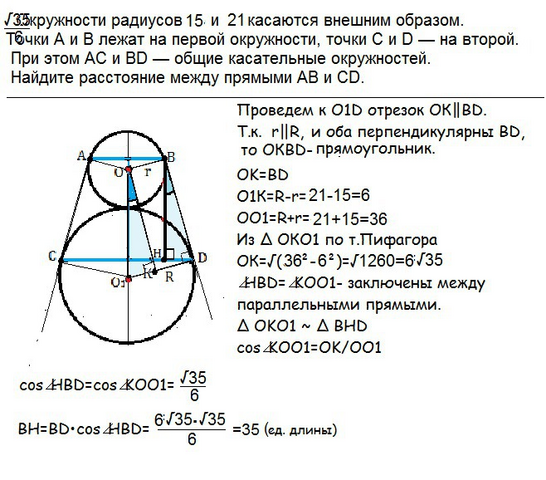
Окружности радиусов 15 и 21 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Решение таких задач почти однотипно.
Искомое расстояние - длина перпендикуляра ВН, опущенного из В на СD.
AB и CD - хорды, перпендикулярны прямой ОО1, содержащей диаметры окружностей.
AB||CD
Пусть центр меньшей окружности - О, большей - О1.
Проведем радиусы r и R в точки касания.
Проведем к О1D отрезок ОК||BD.
Т.к. r||R, и оба перпендикулярны ВD, то ОКВD- прямоугольник.
ОK=BD
О1К=R-r=21-15=6
OO1=R+r=21+15=36
Из ∆ OКО1 по т.Пифагора
OК=√(36²-6²)=√1260=6√35
∠HBD=∠KOO1- их стороны взаимно параллельны.
∆ OKO1 ~ ∆ BHD
cos∠KOO1=OK/OO1
cos∠HBD=cos∠KOO1=(√35):6
BH=BD•cos∠HBD=(6√35)•(√35):6=35 (ед. длины) это искомое расстояние.