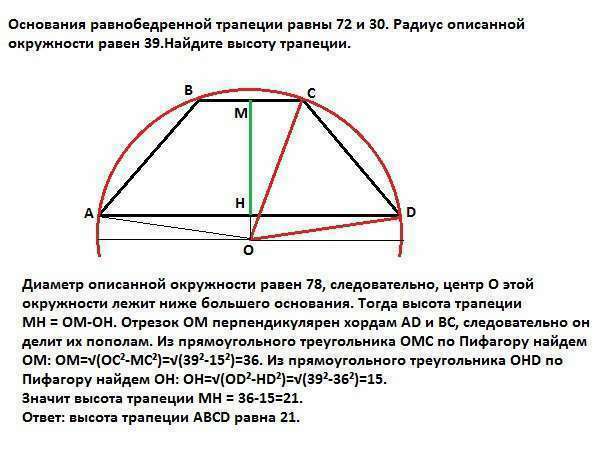
Диаметр описанной окружности равен 78, следовательно, центр О этой окружности лежит ниже большего основания. Тогда высота трапеции
МН = ОМ-ОН. Отрезок ОМ перпендикулярен хордам AD и ВС, следовательно он делит их пополам. Из прямоугольного треугольника ОМС по Пифагору найдем ОМ: ОМ=√(ОС²-МС²)=√(39²-15²)=36. Из прямоугольного треугольника ОНD по Пифагору найдем ОН: ОН=√(ОD²-HD²)=√(39²-36²)=15.
Значит высота трапеции МН = 36-15=21.
Ответ: высота трапеции АВСD равна 21.