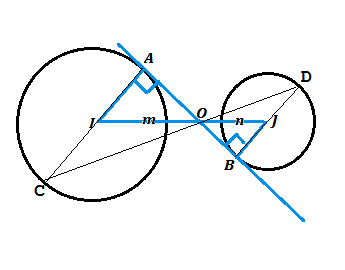
Сделаем рисунок.
АВ - общая касательная.
IJ- отрезок, соединяющий центры.
О - точка пересечения этого отрезка и касательной.
IA - радиус большей окружности, JB - радиус меньшей окружности.
Вариант решения 1)
Как радиусы, проведенные в точку касания, IA и JB перпендикулярны касательной АВ.
Прямоугольные треугольники OIA и OJB подобны по двум углам - прямому и вертикальному при О. Все стороны этих треугольников имеют коэффициент подобия
k=m:n ⇒
IA:JB=m:n
Ясно, чтоотношение диаметров данных окружностей равно отношению их радиусов, т.е. АС:ВD=m:n.
Вариант решения 2)
СА ⊥АВ
BD ⊥АВ ⇒
СА и BD- параллельны.
Углы С и D равны как накрестлежащие при пересечении параллельных прямых секущей.. Углы при О равны, как вертикальные.
Треугольники АСO и DBO подобны по трем углам.
OI OJ- медианы этих треугольников.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Следовательно, отношение диаметров данных окружностей ( гипотенуз треугольников) равно отношению их медиан, т.е. АС:ВD=m:n.