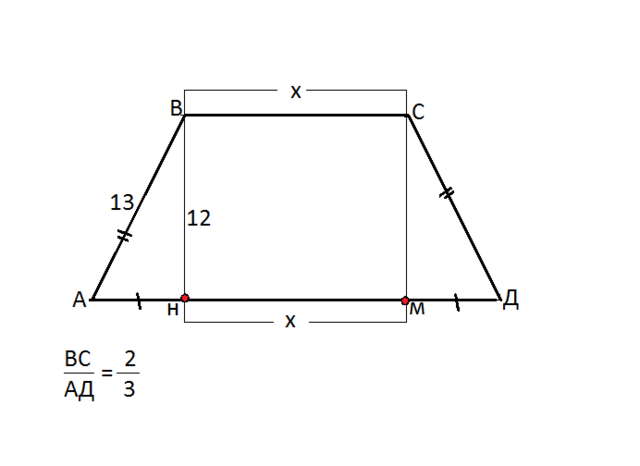
Пусть данная трапеция АВСД,
ВС||АД
АВ=СД=13
Опустим из вершин В и С высоты на АД.
Пусть меньшее основание трапеции ВС=х
Тогда ВС:АД=2/3
ВС=2АД/3
АД=ВС+АН+МД
АН найдем из прямоугольного треугольника АВН по т.Пифагора. АН=5, проверьте ( это треугольник из троек Пифагора, легко запоминается отношение сторон)
АН=МД=5
ВС:АД=2/3
х:(х+10)=2:3
3х=2х+20
х=20
ВС=20 см
Высота, опущенная из тупого угла равнобедренной трапеции делит сторону на отрезки, больший из которых равен полусумме оснований. ⇒
АМ=(ВС+АД):2=АН+НД=25 см
S АВСД=ВН*АМ=12*25=150 см²