Периметр параллелограмма
Р=2*(а+b)=40
полупериметр
р=a+b=40:2=20
Противоположные углы и противоположные стороны параллелограмма равны.
∠ ВАД=∠ВСД.
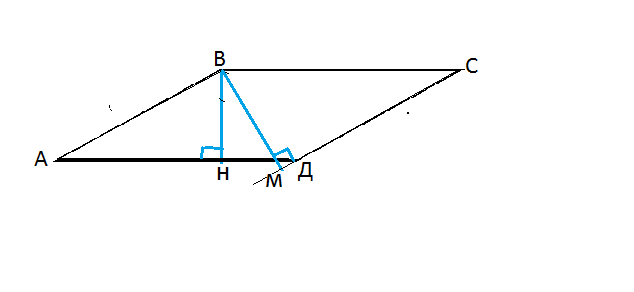
Сделаем рисунок и рассмотрим треугольники АВН и СВМ. Они подобны - прямоугольные с равным острым углом.
ВН:ВМ=АВ:ВС⇒
АВ:ВС=2/3
Пусть АВ=а, ВС=b
a:b=2/3
3a=2b
a=2b/3 Подставим найденное значение а в выражение полупериметра:
a+b=40:2=20
2b/3+b=20
2b+3b=60
5b=60
b=12
a=12*2/3=8
Площадь параллелограмма можно найти по формуле
S=a*h, где h- высота, а- сторона, к которой эта высота проведена.
ВН противолежит углу 30º и равна половине АВ.
ВН=4
S=AД*ВР=12*4=48 см²
Другая формула
S=(a*b*sinα) , где а и b- стороны параллелограмма, α- угол между ними. S=8*12*0,5= 48 см²